Altıgen bir prizmanın kaç kenarı vardır?

Bilmek altıgen bir prizmanın kaç kenarı vardır "kenar", "prizma" ve "altıgen" anlamını bilmek gerekir. İlk iki kavram genel tanımlardır ve üçüncü kavram geometrik figürün şekli ile ilgilidir..

Altıgen hakkında konuşurken altıgen (çokgen) denir. "Hexa" öneki çokgenin altı tarafı olduğunu gösterir.

Kenar, nesnenin bir kenarıdır. Geometrik olarak, bir geometrik şeklin ardışık iki köşesini birbirine bağlayan bir çizgidir..

Bir prizma, paralel ve eşit çokgenli iki bazla sınırlandırılmış geometrik bir figürdür ve yan yüzleri paralelkenarlardır..

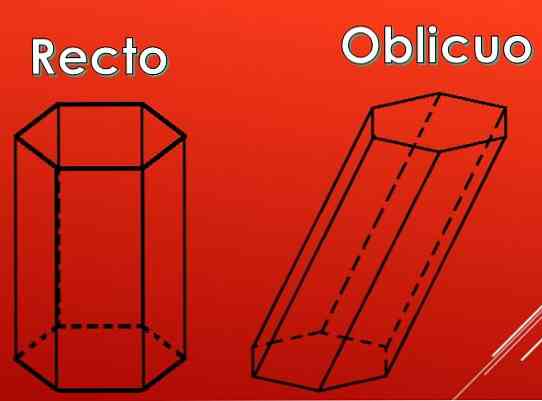
Aşağıdaki resimde, altıgen bir prizmanın yanal yüzeylerinin dikdörtgen olabileceği, ancak paralelogramların da olabileceği görülmektedir..

Paralelkenar tipine göre primler iki tipe ayrılabilir: düz ve eğik.

Altıgen bir prizmanın kenarları nasıl sayılır??

Altıgen bir prizmanın sahip olacağı kenar sayısı, düz veya eğik bir prizma olması durumunda değişmez. Ayrıca, kenar sayısı, kenarların uzunluğuna da bağlı değildir..

Bir altıgen prizmanın kenarlarını saymak birkaç yolla yapılabilir. İşte iki yol:

1- Prizmanın ayrıştırılması

Kenarları saymanın bir yolu, altıgen prizmanın iki tabanından ve yan yüzlerinden ayrıştırılmasıdır. Bu şekilde iki altıgen ve beş iç hatlı bir paralelkenar alırsınız.

Her altıgen altı kenara sahiptir, bu nedenle prizmanın 12'den fazla kenarı olacaktır.

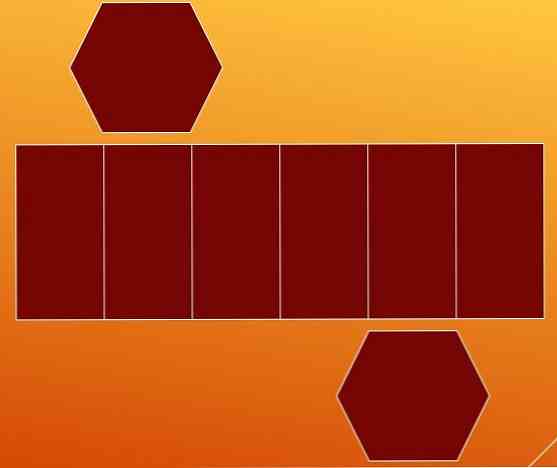
İlk bakışta, paralelkenarın dokuz kenar (yedi dikey ve iki yatay) içerdiği düşünülmektedir. Ancak bu vakayı analiz etmeyi bırakmak uygun.

Paralelkenar, prizma oluşturmak için büküldüğünde, soldaki ilk çizginin sağdaki son çizgiyle birleşeceği ve her iki çizginin de tek bir kenarı temsil ettiği görülebilir..

Peki ya iki yatay çizgi?

Tüm parçalar tekrar bir araya getirildiğinde, yatay çizgiler, her biri, her bir altıgenin altı kenarı ile birleştirilecektir. Bu nedenle, onları ayrı ayrı saymak bir hata olur..

Paralelkenar, başlangıçta sayılan 12 kenarla birlikte toplam 18 kenar veren prizmanın altı kenarını içerir..

2.- Her kenarı yansıtmak

Kenarları saymak daha kolay olan bir başka yol, altıgen prizmaların tabanlarının altıgen olması gerçeğini kullanmaktır, ardından her tabanın altı kenarı vardır..

Öte yandan, bir altıgenin her bir köşesinden, diğer altıgenin karşılık gelen köşesine tek bir kenar yansıtılmaktadır; yani, bir kaideyi diğeriyle birleştiren altı kenar vardır..

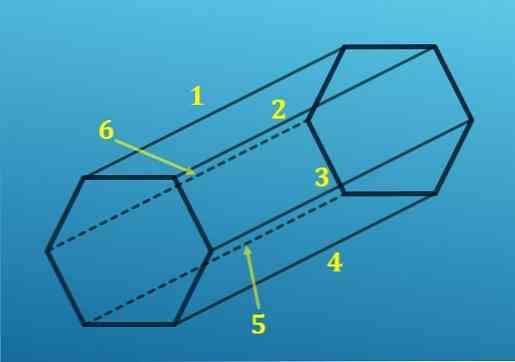
Tüm kenarları ekleyerek toplam 18 kenar elde edersiniz..

Sonuç

Bir prizmanın kenar sayısının, poligonun kendisini oluşturan kenar sayısının üç katına eşit olduğu gösterilebilir..

Bu nedenle, bir pentagonal prizma 3 x 5 = 15 kenara sahip olacak, heptagonal bir prizma 3 x 7 = 21 kenara sahip olacak ve böylece herhangi bir prizmaya uygulanabilir.

referanslar

1. Billstein, R., Libeskind, S., ve Lott, J.W. (2013). Matematik: temel eğitim öğretmenleri için problem çözme yaklaşımı. López Mateos Editörleri.
2. Fregoso, R.S., ve Carrera, S.A. (2005). Matematik 3. Editoryal Progreso.
3. Gallardo, G. ve Pilar, P.M. (2005). Matematik 6. Editoryal Progreso.
4. Gutiérrez, C.T., & Cisneros, M.P. (2005). 3. Matematik Kursu. Editoryal Progreso.
5. Kinsey, L. ve Moore, T. E. (2006). Simetri, Şekil ve Mekan: Geometri İle Matematiğe Giriş (resimli, yeniden basım.). Springer Bilim ve İş Medyası.
6. Mitchell, C. (1999). Göz Kamaştırıcı Matematik Hattı Tasarımları (Resimli ed.). Skolastik A.Ş..
7. R., M.P. (2005). 6º çizerim. Editoryal Progreso.