Colinear Sistem ve Örnekler
colinear vektörleri Bunlar mevcut üç vektör türünden biridir. Aynı yönde veya etki çizgisinde bulunan vektörlerle ilgilidir. Bunun anlamı şudur: birbirlerine paralel olan düz çizgiler halinde düzenlenirlerse iki veya daha fazla vektör collinear olacaktır.
Bir vektör, bir vücuda uygulanan miktar olarak tanımlanır ve bir yöne, bir algıya ve ölçeğe sahip olması ile karakterize edilir. Vektörler düzlemde veya uzayda bulunabilir ve farklı türlerde olabilir: koliner vektörler, eşzamanlı vektörler ve paralel vektörler.

indeks
- 1 colineal vektörleri
- 2 özellikleri
- 2.1 Örnek 1
- 2.2 Örnek 2
- 2.3 Örnek 1
- 3 Collinear vektör sistemi
- 3.1 Karşı duyulara sahip arızalı vektörler
- 3.2 Aynı anlamda Collinear vektörleri
- 3.3 Eşit büyüklükte ve zıt duyulara sahip arsenel vektörler
- 4 Eş zamanlı ve eşzamanlı vektörler arasındaki fark
- 5 Kaynakça
Collinear vektörleri
Bir vektörün eylem çizgisi, her bir vektörün büyüklüğünden ve anlamından bağımsız olarak, diğer tüm vektörlerin tam olarak aynı hareket çizgisiyse, vektörler ortaktır..
Vektörler, matematik, fizik, cebir gibi farklı alanlarda ve aynı zamanda vektörlerin, sadece yönleri aynı olduğunda, sadece anlamlarının aynı olup olmadığına bakılmaksızın collinear olduğu geometride, temsiller olarak kullanılır..
özellikleri
- İki veya daha fazla vektör, koordinatlar arasındaki ilişki eşitse.
Örnek 1
M = m_x; vektörlerine sahibiz; m_y ve n = n_x; n_y. Bunlar şu durumlarda collinear:
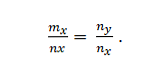
Örnek 2
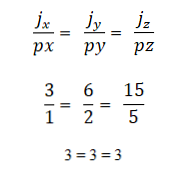
- Ürün veya vektör çarpımı sıfıra (0) eşitse, iki veya daha fazla vektör collinear'dır. Bunun nedeni, koordinat sisteminde, her vektörün kendi koordinatlarıyla tanımlanmasıdır ve eğer bunlar birbirleriyle orantılıysa, vektörler eşdüzey olacaktır. Bu şu şekilde ifade edilir:
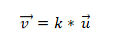
Örnek 1
A = (10, 5) ve b = (6, 3) vektörlerine sahibiz. Eşli olup olmadıklarını belirlemek için, çapraz ürünlerin eşitliğini sağlayan belirleyici teori uygulanır. Bu şekilde yapmanız gerekenler:
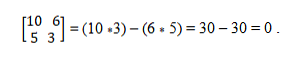
Colinear vektör sistemi
Colinear vektörleri, uygulama noktasından geçmeleri gerektiği ve belli bir ölçek veya uzunluk olan modülün yönünü ve anlamını kullanarak grafiksel olarak temsil edilir..
Kolinik vektörler sistemi iki veya daha fazla vektör bir nesneye veya gövdeye etki ettiğinde, bir kuvveti temsil ederken ve aynı yönde hareket ettiğinde oluşur..
Örneğin, bir vücut üzerine iki koliner kuvveti uygulanırsa, bunların sonucu yalnızca hareket ettikleri yöne bağlı olacaktır. Üç dava var, bunlar:
Karşı duyulara sahip arsener vektörleri
İki collinear vektörün sonucu, bunların toplamına eşittir:
R = Σ F = F1 + F2.
örnek
İki kuvvet F arabasına etki ederse F1 = 40 N ve F2 = Ters yönde 20 N (resimde gösterildiği gibi), sonuç şöyledir:
R = Σ F = (- 40 N) + 20N.
R = - 20 N.
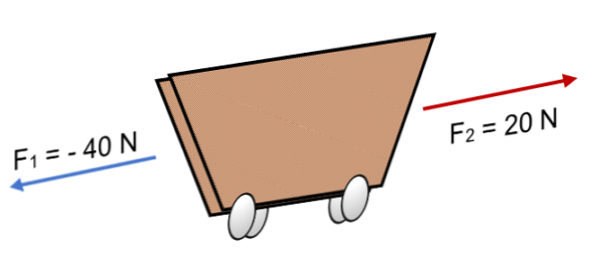
Aynı anlamda Collinear vektörleri
Elde edilen kuvvetin büyüklüğü, kolinear vektörlerin toplamına eşit olacaktır:
R = Σ F = F1 + F2.
örnek
İki kuvvet F arabasına etki ederse F1 = 35 N ve F2 = 55 N aynı yönde (resimde gösterildiği gibi), sonuç şöyledir:
R = Σ F = 35 N + 55N.
R = 90 N.
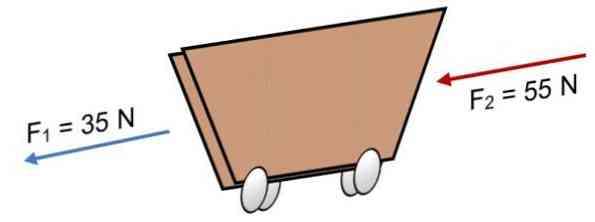
Olumlu sonuç, collinear vektörlerin sola doğru hareket ettiğini gösterir..
Eşit büyüklükte ve zıt duyulara sahip arsenel vektörler
İki collinear vektörün ortaya çıkan sonucu collinear vektörlerin toplamına eşit olacaktır:
R = Σ F = F1 + F2.
Kuvvetler aynı büyüklükte olduğu için ancak tersi yönde - ki, biri pozitif diğeri negatif olacak - iki kuvvet eklendiğinde sonuç sıfıra eşit olacaktır..
örnek
İki kuvvet F arabasına etki ederse F1 = -7 N ve F2 = 7 N, aynı büyüklükte fakat ters yönde (resimde gösterildiği gibi) sonuç şöyledir:
R = Σ F = (-7 N) + 7N.
R = 0.
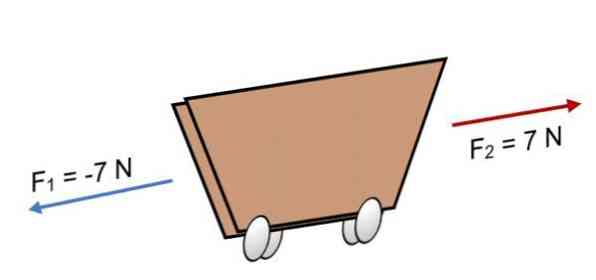
Elde edilen 0'a eşit olduğu için, vektörlerin birbirine karşı dengeli olduğu ve dolayısıyla vücudun dengede veya istirahatta olduğu anlamına gelir (hareket etmeyecek).
Eş zamanlı ve eşzamanlı vektörler arasındaki fark
Collinear vektörleri, aynı çizgide aynı yöne sahip olmaları veya bir çizgiye paralel olmaları ile karakterize edilir; yani, onlar doğrudan paralel çizgiler vektörlerdir.
Öte yandan, eşzamanlı vektörler tanımlanmıştır, çünkü tek bir noktadan yakalanan farklı eylem çizgilerindedirler..
Başka bir deyişle, aynı menşe veya varış noktasına sahiptirler - modülleri, yönleri veya yönleri ne olursa olsun - aralarında bir açı oluşturarak.
Eşzamanlı vektörlerin sistemleri, kuvvetlerin paralelkenarının yöntemi ve kuvvet poligonunun yöntemi olan matematiksel yöntemlerle veya grafiklerle çözülür. Bunlar sayesinde, bir vücudun hareket edeceği yönü belirten, elde edilen vektörün değeri belirlenir..
Temel olarak, colinear vektörleri ve eşzamanlı vektörler arasındaki temel fark, hareket ettikleri eylem çizgisidir: collinear olanlar aynı çizgide hareket ederken, aynı zamanda farklı olanları da.
Yani, collinear vektörleri tek bir düzlemde, "X" veya "Y"; ve her iki düzlemde eşzamanlı hareket, aynı noktadan başlayarak.
Toplayıcı vektörler aynı anda olduğu gibi bir noktada değildir, çünkü birbirlerine paraleldirler..
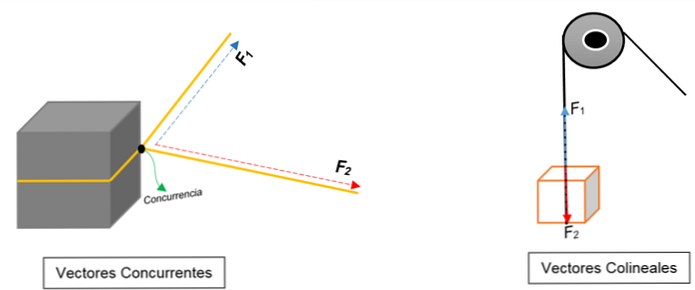
Soldaki resimde bir blok görebilirsiniz. Bir iple bağlanır ve düğüm ikiye böler; farklı yönlere ve farklı kuvvetlere doğru çekildiğinde, blok aynı yöne doğru hareket eder.
Modüllerinden, algılarından veya yönlerinden bağımsız olarak bir noktada (blok) aynı fikirde olan iki vektör temsil edilir..
Bunun yerine, sağ resimde bir kutu kaldıran bir kasnak görünür. İp, hareket hattını temsil eder; çekildiğinde, üzerine iki kuvvet (vektör) etki eder: bir gerilme kuvveti (bloğu tırmanırken) ve diğer kuvvet, bloğun ağırlığını uygulayan kuvvet. Her ikisi de aynı yöne ancak ters yöne sahiptir; bir noktada hemfikir değil.
referanslar
- Estalella, J. J. (1988). Vektör analizi. Cilt 1.
- Gupta, A. (s.f.). Tata McGraw-Hill Eğitim.
- Jin Ho Kwak, S.H. (2015). Doğrusal Cebir. Springer Bilim ve İş Medyası.
- Montiel, H.P. (2000). Teknolojik Bakalorya için Fizik 1. Patria Editör Grubu.
- Santiago Burbano de Ercilla, C.G. (2003). Genel fizik Editoryal Tebar.
- Sinha, K. (s.f.). Matematik Ders Kitabı XII Cilt 2. Rastogi Yayınları.


